- Gleichgewicht
Gleichgewicht eines Kräftesystems, das an einem System von Massenpunkten angreift, ist der Zustand desselben, in dem es keine Wirkung auf den Bewegungszustand des Punktsystems ausübt. Ein im Gleichgewicht befindliches System von Kräften gibt keine Aenderung des Beschleunigungszustands. Gleichgewicht ist ein Zustand des Kräftesystems, nicht des Punktsystems; letzteres hat Gleichgewichtslagen, in denen das betreffende Kräftesystem im Gleichgewicht[560] ist. Gleichgewicht des Kräftesystems und Ruhezustand des Punktsystems sind sorgfältig zu unterscheiden; ersteres kann mit Bewegungszustand oder mit Ruhezustand des letzteren verbunden sein. Das Gleichgewicht des Kräftesystems ist abhängig von der Beschaffenheit des Punktsystems, und die Verhältnisse, unter denen es eintritt, sind andre, je nachdem dieses unveränderlich oder veränderlich, frei oder an Bedingungen gebunden ist.
Die allgemeinste Methode zur Ermittlung der Gleichgewichtsbedingungen bietet das Prinzip der virtuellen Geschwindigkeiten (s.d.). Hiernach befindet sich ein Punktsystem im Gleichgewicht, wenn bei jeder unendlich kleinen mit den Bedingungen der Beweglichkeit des Systems verträglichen Verschiebung die algebraische Summe der Arbeiten der wirkenden Kräfte Null (eigentlich unendlich klein von höherer Ordnung) wird.
Ist diese unendlich kleine Summe der Arbeiten der wirkenden Kräfte für alle möglichen Verschiebungen aus einer Lage negativ, so ist das Gleichgewicht in dieser Lage stabil, andernfalls labil. Haben die wirkenden Kräfte ein Potential, so erfüllt dieses für eine Gleichgewichtslage des Systems die notwendigen Bedingungen eines Extremums; erfüllt es außerdem noch die hinreichenden Bedingungen eines Minimums, so ist das Gleichgewicht stabil. Sind die wirkenden Kräfte ausschließlich Schwerkräfte, so ist das Potential proportional der Höhe des Gesamtschwerpunktes; diese muß also im Falle des stabilen Gleichgewichtes ein Minimum sein. Aehnlich liegt die Sache bei elastischen Kräften, wobei im Falle des Gleichgewichtes die Formänderungsarbeit ein Minimum wird.
Ein im Gleichgewicht befindliches Kräftesystem kann den Bewegungszustand des Punktsystems, an dem es angreift, nicht ändern, welches derselbe auch sein mag. Daher kann dieser geändert werden, ohne daß das Gleichgewicht der Kräfte gestört wird, solange dadurch an der Intensität, Richtung und Lage der Kräfte sich nichts ändert. Findet daher Gleichgewicht von Kräften an einem veränderlichen System statt, so besteht dasselbe fort, wenn das System im ganzen oder in einzelnen Teilen unveränderlich wird, z.B. erstarrt. Denn dadurch wird bloß seine Beweglichkeit eingeschränkt und es werden gewisse vorher mögliche Bewegungszustände ausgeschlossen. Daher bestehen die Bedingungen des Gleichgewichts von Kräften am unveränderlichen System auch für das veränderliche System als notwendige, aber nicht als hinreichende Bedingungen. Ebenso folgt, daß das Gleichgewicht an einem beliebigen veränderlichen System fortbesteht, wenn Teile desselben unbeweglich werden. Denn auch durch das Festwerden einzelner Teile wird bloß die Beweglichkeit eingeschränkt.
Für das freie unveränderliche Punktsystem sind sechs Bedingungen des Gleichgewichts notwendig und hinreichend, nämlich, daß die Summe der Projektionen aller Kräfte auf drei nicht einer Ebene parallele Achsen und die Summe ihrer Momente in bezug auf dieselben Null sei. Sind X, Y, Z die Komponenten einer Kraft, parallel drei zueinander rechtwinkligen Koordinatenachsen, und x, y, z die Koordinaten ihres Angriffspunktes, so sind diese sechs Bedingungen des Gleichgewichts:
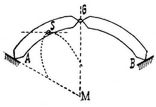
(vgl. Art. Aequivalenz der Kräfte, Bd. 1, S. 86). Diese Bedingungen sprechen den Satz aus, daß die Reduktionsresultante und das resultierende Achsenmoment des Kräftesystems verschwinden muß. Dieselben sind verschiedener andrer Einkleidungen fähig, z.B. in dem Satze, daß die Summe der Tetraeder, gebildet mit einer beliebigen Strecke des Raumes und den einzelnen Strecken, welche die Kräfte darstellen als Gegenkanten, verschwinden müsse. Als Beispiel für die Untersuchung der Stabilität eines beweglichen Systems betrachten wir (s. die Figur) zwei symmetrische starre Körper, die im Punkte G gelenkig verbunden sind und in den Punkten A und B auf glatten ebenen Gleitflächen ruhen. Die Körper seien der Schwere unterworfen; S sei der Schwerpunkt des einen von ihnen. Zu den möglichen Verschiebungen des Systems gehören auch jene, bei denen die Symmetrie aufrechterhalten bleibt, der Punkt G sich in einer Lotlinie hebt oder senkt und die Punkte A und B um gleiche Stücke auf ihren Gleitflächen ab- oder aufwärts gleiten. Bei einer solchen Bewegung beschreibt der Schwerpunkt S eine Ellipse, deren Mittelpunkt M im Schnittpunkt des Lotes durch G und der Gleitfläche durch A ist (vgl. Bewegung von Cardano, Bd. 1, S. 767). Im Falle des Gleichgewichts ist die Tangente im Punkte S an die Ellipse horizontal; bei einer kleinen Verschiebung verändert also S seine Höhe nur um ein Unendlichkleines zweiter Ordnung. Dieses ist aber negativ, da die Ellipse nach unten zu hohl ist. Der Schwerpunkt sinkt also bei jeder solchen Bewegung, also kann das Gleichgewicht nicht stabil sein. Eine nach obigem System konstruierte Gelenkbrücke kann nur durch die Reibung im Gleichgewicht sein und muß nach Aufhebung derselben bei der geringsten Störung einstürzen.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.