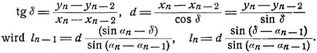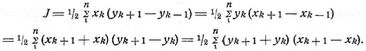- Polygonometrie
Polygonometrie, die Lehre von der Ausmessung der Polygone.
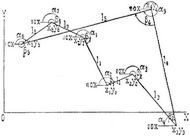
Ein polygonaler Zug bestehe aus den (n + 1) Punkten x0 y0, x1y1, ... xnyn, die durch die Seiten von den Längen l1l2 ... ln und den Richtungswinkeln α1 α2 ... αn verbunden sind. Die Polygonwinkel seien ß1ß2 ... ßn – 1. Sind die Seiten und die Polygonwinkel nebst den Koordinaten x0y0 des Anfangspunkts und dem Richtungswinkel α1 der ersten Seite gegeben, so ist α2 = α1 + 180° + β1; α3 = α2 +180° + β2; ... αn = αn – 1 + 180° + βn – 1; ferner x1 = x0 + l1 cos α1; x2 = x1 + l2 cos α2 ... xn = xn – 1 + ln cos αn; y1 = y0 + l1 sin α1; y2 = y1 + l2 sin α2 ... yn = yn – 1 + ln sin αn. Fällt der Punkt xnyn mit x0y0 zusammen, so entsteht ein geschlossenes Polygon. Die algebraische Summe der Projektionen der Seiten eines geschlossenen Polygons auf eine beliebige Achse ist Null.
a) In einem Polygon sind alle Seiten außer ln – 1 und ln gegeben, ferner alle Winkel außer ßn – 1; ferner ist xnyn und α1 gegeben. Nach Berechnung von x1y1, x2y2 ... xn – 2, yn – 2 und α2 ... αn – 1 wird αn = αn – 1 + 180 + βn – 1; α1 = αn + 180 + βn, woraus sich αn und ßn – 1 ergeben. Mit
b) In einem Polygon sind alle Seiten außer ln und alle Winkel außer ßn – 1 und ßn gegeben; ferner ist xnyn und α1 gegeben. Nach Berechnung von x1y1 ... xn – 1, yn – 1 und α2 ... αn – 1 hat man
c) In einem Polygon sind alle Seiten und die Winkel außer βn – 2, ßn – 1, ßn gegeben; ferner ist xnyn und α1 gegeben. Man berechnet x1y1 ... xn – 2 yn – 2, α2 ... αn – 2. Man setzt nun
berechnet sodann die Winkel γn – 2, γn – 1, γn des Dreiecks aus den Seiten ln, d, ln – 1. Alsdann, ist αn – 1 = δ ± γn – 2 αn = δ ± γn, also zwei verschiedene Lösungen. Endlich ist ßn – 2 = αn – 1 – αn – 2 + 180°; ßn – 1 = αn – αn – 1 + 180°; ßn = α1 – αn + 180°.
Für die Fläche eines Polygons, dessen Ecken die Koordinaten x1y1 ... xnyn haben, ist:
Die Summen sind über k von 1 bis n zu nehmen.
Literatur: [1] Hammer, Lehrbuch der ebenen und sphärischen Trigonometrie, Stuttgart 1885, S. 187–205. – [2] Spitz, Lehrbuch der ebenen Polygonometrie, 2. Aufl., Leipzig 1881. – [3] Wellisch, Die Berechnungen in der praktischen Polygonometrie, Wien 1893.
Wölffing.
http://www.zeno.org/Lueger-1904.